La geometria della Natura – I frattali

1) http://www.youtube.com/watch?v=VHyoYEqk0-Y
2) http://www.youtube.com/watch?v=JM5530_Rffg&feature=related
3) http://www.youtube.com/watch?v=1ntyNg6L6EA&feature=related
4) http://www.youtube.com/watch?v=P2utymFOJLY&feature=related
5) http://www.youtube.com/watch?v=Y0qFCIsvGUc&feature=related
6) http://www.youtube.com/watch?v=7E81w1fS3Zs&feature=related

Il domino e memory

Tantissimi giochi sono impostati sull’uso di forme geomentriche, ecco un altro esempio abbinato alla matematica: il domino.

Il domino è un gioco da tavolo che si svolge utilizzando 28 tessere. Queste sono tutte suddivise in due sezioni recanti dei punteggi segnati con dei pallini, da 0 (nessun pallino) a 6. Si può giocare in 2 oppure in 4 persone.
Si inizia rovesciando a faccia in giù sul tavolo le tessere e se ne distribuiscono 7 a testa, senza farle vedere all’avversario. Se si gioca in due le restanti 14 vanno lasciate a faccia in giù, serviranno in seguito; se si gioca in 4 una volta distribuite 7 tessere per ciascun giocatore saranno esaurite. Il primo giocatore viene scelto a caso (oppure è chi ha il doppio 6 se si gioca in 4) e inizia a disporre la prima tessera sul tavolo; poi il turno passa alla persona che segue alla sua sinistra: questi potrà mettere una sua tessera attaccata a quella che c’è già solo se ne ha una col punteggio uguale a una delle due sezioni. La forma del “serpente” di tessere è libera. Se un giocatore non può attaccare una tessera, passa il turno se si gioca in 4; oppure pesca da quelle rimaste e passa il turno a meno che non sia possibile disporre quella pescata sul tavolo. Vince chi finisce per primo le tessere.

Un altro gioco classico, che tutti noi abbiamo sicuramente incontrato è memory!

Memory, noto anche come coppie, è un popolare gioco di carte che richiede concentrazione e memoria. Nel gioco, le carte sono inizialmente mescolate e disposte coperte sul tavolo. I giocatori, a turno, scoprono due carte; se queste formano una “coppia”, vengono incassate dal giocatore di turno, che può scoprirne altre due; altrimenti, vengono nuovamente coperte e rimesse nella loro posizione originale sul tavolo, e il turno passa al prossimo giocatore. Vince il giocatore che riesce a scoprire più coppie.

Se si gioca con un mazzo di carte tradizionale, per “coppia” si intendono di solito due carte dello stesso valore e dello stesso seme; esistono tuttavia anche mazzi di carte dedicati, composti di un certo numero di coppie identiche.
I primi turni del gioco hanno un andamento ovviamente casuale. Man mano che le carte vengono scoperte e rimesse in gioco, i giocatori dovrebbero iniziare a ricordare la posizione di alcune, e tentare quindi di comporre le coppie. In generale, un giocatore che pensi di aver localizzato una coppia dovrebbe scoprire prima la carta di cui è meno certo; in caso di fallimento, in questo modo, può evitare di scoprire una carta che conosce già (con l’effetto ulteriore di “rinfrescare la memoria” agli avversari).

Se vogliamo invece utilizzare mattoncini? Il LEGO

Possiamo giocare non solo con l’utilizzo di quadrati ma anche di rettangoli, semplici mattoncini… come?
Con i LEGO! Un gioco che tutti conoscono e che tutti, almeno una volta, hanno utilizzato nella loro vita.

LEGO è un produttore di giocattoli danese, noto internazionalmente per la sua linea di mattoncini assemblabili.

L’azienda, fondata nel 1916 da Ole Kirk Christiansen, ha iniziato a produrre i famosi mattoncini a partire dal 1949, ma soltanto dal 1958 essi assumono la particolare forma che ne caratterizza ancora oggi gli assemblaggi.

Dalla iniziale serie classica, l’azienda ha nel tempo realizzato anche la serie Duplo, dedicata ai più piccoli, dai mattoncini più grandi (quindi non ingeribili) e più facilmente incastrabili, e la serie Technic rivolta ai più grandi, dalla gran quantità di pezzi meccanici, ingranaggi, motori, e perfino programmabile. Più recentemente il marchio è stato applicato con successo, sempre rimanendo fedele a se stesso, anche ad alcune serie di videogiochi e film (Bionicle 1, 2, 3, 4).

Poiché i LEGO hanno come consumatore un pubblico di bambini, il design dei giocattoli è giocoforza imperniato sull’ergonomia, affinché siano utilizzabili intuitivamente da chiunque senza l’ausilio di istruzioni. Per ottenere questo risultato, per ogni specifico componente è necessario impegnare un alto livello di specializzazione ingegneristica.

Una delle caratteristiche chiave dei mattoncini LEGO è il far parte di un “sistema”. Ogni nuova serie o scatola è compatibile con il resto del sistema; ciascun pezzo, indipendentemente dalle sue dimensioni, forma o funzione, si incastra con la maggioranza degli altri LEGO. Per esempio, gli ingranaggi e i meccanismi a motore della serie Technic, pensati per ragazzi e adolescenti, possono essere collegati a mattoncini DUPLO pensati per bimbi di tre anni. Questa caratteristica consente al sistema LEGO di evolvere e di adattarsi alle varie fasi della crescita del bambino, fino alla maggiore età.

La fusione della materia prima avviene in due impianti: in Danimarca e Svizzera. Le decorazioni ed il confezionamento si svolgono negli stabilimenti in Danimarca, Svizzera, USA, Corea del Sud e Repubblica Ceca. La media di produzione annuale è di circa 20 miliardi di mattoncini all’anno, ovvero circa 2,3 milioni all’ora.

Mattoncini, piattaforme, assi, ometti, e tutti gli altri elementi del sistema LEGO, sono prodotti con dimensioni dalla tolleranza infinitesimale poiché, quando vengono incastrati, devono avere la giusta coesione e mantenerla. Per fare in modo che fra i pezzi vi sia il giusto incastro, la tolleranza di produzione è di 2 millesimi di millimetro (0,002mm), o di 8 milionesimi di pollice (0,00008″).

Per mantenere quest’alta qualità, è necessario utilizzare particolari impianti di fusione con produzione a quantità limitata e macchine ad alta precisione. Gli stampi ad iniezione sono equipaggiati con sensori che rilevano le minime variazioni di pressione e temperatura. Personale specializzato, inoltre, controlla l’uscita degli stampi, assicurandosi che non vi siano anomalie nelle misure o nella tinta del colore. Secondo quanto dichiarato da LEGO, solo 18 pezzi su un milione non rispettano gli standard qualitativi. È grazie a questa cura nella produzione che i LEGO hanno mantenuto un così alto grado di qualità nel corso degli anni; è anche una delle ragioni per cui pezzi prodotti negli anni settanta si incastrano con pezzi prodotti più recentemente.

Il cubo di Rubrik

Ecco un esempio di come si può giocare e divertirsi comodamente a casa, utilizzando semplici quadratini che, composti tra loro, danno sempre quadrati più grandi: IL CUBO DI RUBRIK.

Il Cubo di Rubik, o Cubo magico (Rubik-kocka in ungherese) è un celebre rompicapo (in particolare un twisty puzzle) inventato dal professore di architettura e scultore ungherese Ernő Rubik nel 1974. Chiamato originariamente Magic Cube (Cubo magico) dal suo inventore, il rompicapo fu rinominato in Rubik’s Cube (Cubo di Rubik) dalla Ideal Toys nel 1980 e nello stesso anno vinse un premio speciale dalla giuria dello Spiel des Jahres in Germania, unico solitario premiato nella storia del premio. È il giocattolo più venduto della storia, con circa 300 milioni di pezzi venduti, considerando anche le imitazioni.
Il Cubo di Rubik presenta 9 quadrati su ogni faccia, per un totale di 54 quadrati. Solitamente i quadrati differiscono tra loro per il colore, con un totale di 6 colori differenti. Quando il Cubo di Rubik è risolto, ogni faccia ha tutti i nove quadrati dello stesso colore. Il rompicapo ha celebrato il 25º anniversario nel 2005, anno nel quale è stata presentata una versione speciale del cubo, con il logo ufficiale – Rubik’s Cube 1980-2005 – stampato su un quadrato di colore bianco.

Lo scopo del gioco è di risalire alla posizione originale dei cubetti portando il cubo ad avere per ogni faccia un colore uguale. Il cubo, nella versione 3x3x3, può assumere ben 43.252.003.274.489.856.000 combinazioni possibili di cui solo una è quella corretta. Il cubo, nella versione 2x2x2, può assumere 3.674.160 combinazioni possibili, di cui solo una è quella corretta.

Il più intuitivo metodo risolutivo è il metodo a strati. Consiste nella risoluzione strato per strato. Vi sono 7 passi da effettuare (croce, angoli primo strato, secondo strato, orientamento spigoli, orientamento angoli, permutazione spigoli, permutazione angoli). Questo metodo ha il vantaggio di dover memorizzare pochi algoritmi, ma non è adatto per lo speedcubing, perché risulta molto più lento rispetto ai metodi più avanzati. Infatti difficilmente con questo metodo si riesce a scendere sotto il minuto, mentre con quelli degli speedcubing la media è di 15-20 secondi.

Questo metodo di risoluzione si può riassumere così: croce, formare una faccia, completare il secondo strato, completare l’ultimo strato e la faccia opposta di quella di partenza.

* Croce: la croce è il punto di partenza per completare il cubo con questo metodo. Per fare la croce non esistono algoritmi ma bisogna andare ad inutito. Le parti che formeranno la croce saranno la parte centrale di una faccia e gli spigoli a essa adiacenti. Inoltre bisogna tenere conto che lo spigolo deve essere allineato sopra la corrispettiva faccia; per esempio lo spigolo bianco-arancione, la parte bianca andrà vicino la faccia centrale bianca e quello arancione deve essere allineato alla parte centrale arancione.
* Prima faccia: dopo aver fatto la croce ed aver allineato bene gli spigoli con le loro corrispondenti facce centrali, si devono portare gli angoli sulla faccia dove si è fatta la croce per completarla. Ogni angolo ha 3 quadratini; uno dei quali sarà quello che dovrà essere portato sulla faccia di partenza. Gli altri due colori corrispondono a due delle facce laterali, le quali avranno la faccia centrale e lo spigolo sopra già allineato. Ogni angolo deve essere posizionato tra i rispettivi colori delle facce centrali; ad esempio l’angolo bianco-rosso-blu andra posizionato tra la faccia con il centro rosso e quello blu. Per posizionare gli angoli senza disfare la croce bisogna semplicemente muovere i due strati della faccia con la croce, che non sono interessati di quell’angolo, verso il basso e poi riposizionarlo come prima. Così facendo la croce non sarà distrutta e l’angolo sarà messo al suo posto. Dopo aver completato tutti e quattro gli angoli la faccia sarà completata e anche il primo strato, ovvero quello che si trova nelle facce laterali rispetto a quella di partenza e che è direttamente collegato con essa (posizionato sopra il centro della faccia laterale).
* Secondo strato: il secondo strato coinvolge le quattro facce laterali. Il secondo strato è quello che comprende il quadratino centrale di una faccia per completarlo bisogna posizionare gli spigoli in quello stato. Qui ci troviamo davanti al primo algoritmo cioè un movimento fisso che permette di posizionare un determinato spigolo nella sua posizione (ricordiamo che per completare la croce e la prima faccia non c’erano algoritmi, ma andava ad intuito). L’algoritmo non è sempre lo stesso, infatti ce ne sono diversi per completare questo strato, ma sono tutti efficienti. Nel secondo strato abbiamo già la parte centrale posizionata e quindi si deve mettere a posto gli spigoli ad essa adiacenti; ad esempio nella faccia rossa, che è collegata con quelle blu e verdi, bisogna posizionare gli spigoli rosso-blu e rosso-verdi adiacenti alla faccia centrale. Dopo averlo completato ci saranno da completare il terzo strato e l’ultima faccia.
* Completare il cubo: questo passaggio è il più difficile non solo perché in alcuni metodi per risolvere questo strato ci sono quattro algoritmi, ma anche perché è la più lunga da completare. Si inizia formando una croce nella faccia opposta a quella di partenza e quella già completata (la faccia opposta al bianco è il giallo, quella del rosso è l’arancione, quella del blu è il verde. Questo vale per la versione originale del cubo, nelle altre versioni i colori possono essere differenti). La croce si forma con un algoritmo così da non distruggere la faccia già fatta e il secondo strato. La croce non deve essere rigorosa come quella della prima faccia; infatti nella prima gli angoli andavano posizionati dopo, in questa gli angoli possono essere anche tenuti insieme alla croce. Dopo aver fatto la croce si guarda lo spigolo che comprende il quadratino della croce nella faccia opposta a quella di partenza e la faccia centrale del terzo strato, l’ultimo da completare. Lo spigolo deve andare sopra gli alti due già posizionati. Gli spigoli devono essere tutti posizionati correttamente per andare aventi. Se invece sono posizionati male si prende una faccia in cui lo spigolo è posizionato bene e si parte con un algoritmo per posizionarli tutti bene. Il secondo caso è quello più frequente e anche in caso di spigoli posizionati male con l’algoritmo che si farà non distruggerà il lavoro fatto prima. Ora si devono posizionare gli angoli. Qui dobbiamo trovare dagli angoli posizionati bene o orientati bene. Posizionati bene significa che i tre quadratini dell’angolo si trovano in mezzo alle tra facce corrispondenti ma in una posizione sbagliata, orientati bene vuol dire che la posizione che stavamo parlando prima è giusta. Ad esempio l’angolo giallo-blu-rosso è posizionato bene quando il quadratino giallo è sulla faccia rossa, quello rosso su quella blu e quello blu su quella gialla. Orientato bene vuol dire che il quadratino giallo è sulla faccia gialla, quello blu su quelle blu, quello rosso su quella rossa. Partendo da un angolo posizionato o orientato bene si parte con un altro algoritmo che andrà a posizionarli bene tutti. Può accadere che siano già tutti posizionati bene. In casi molto rari accade che durante questo algoritmo gli angoli vengono anche orientati bene completando così il cubo saltando un passaggio. L’ultimo passaggio consiste nell’orientare bene tutti gli angoli completando il terzo strato e la faccia opposta a quella di partenza. Qui ci vuole ancora un algoritmo, non difficile da memorizzare, ma molto rischioso perché questo algoritmo non manterrà fisse le posizioni della faccia di partenza e il secondo strato ma le scombinerà per poi rimetterle a posto. Dopo questo algoritmo il cubo sarà completato.

Ora non so bene voi……… ma io ancora non lo so fare! =)

Giochi con la geometria

http://www.istitutoarici.it/metelli/giochi/giochi_geomet.htm

Viaggio al centro della geometria

Ho trovato un bellissimo sito con giochi che riguardano soprattutto la geometria e le forme!
Riporto il link con la pagina di presentazione!

Misurare, ritagliare, manipolare, riunire, capire.
Al di là delle forme, la meccanica del sapere…

Ad ognuno il suo rompicapo!

Nato dalla nostra esperienza di designer di giochi educativi appassionati di matematica (da anni insegniamo, tramite il nostro laboratorio itinerante, la matematica metaforica), questo sito è, prima di tutto, fatto per divertire ed è rivolto ai grandi e ai piccoli, agli insegnanti e agli amatori di enigmi, insomma proprio a tutti!

“Archimedes’ Lab” è un’officina della creatività che propone rompicapi originali, curiosità matematiche, illusioni ottiche inedite, che stimola e assiste chi voglia saperne di più sulla ‘matematica ricreativa’ in generale e sui puzzle in particolare: la loro storia, la loro origine, ecc.

Chi ha detto che le mani sono gli occhi della mente? È vero, la gran parte dei giochi d’ingegno raccolti in questo sito si possono risolvere con le mani utilizzando materiale facilmente reperibile: carta, matita, forbici, a volte un po’ di colla, un pezzo di corda… Seguendo le istruzioni, si possono anche riprodurre alcuni rompicapi per divertirsi, stimolare la propria materia grigia, o per sfidare gli amici… “Archimedes’ Lab” è una vera ‘Palestra della Mente’!

Per aiutarvi a risolvere i giochi matematici del nostro sito, ecco qualche consiglio:

• Diffidate di ciò che sembra facile, non sempre lo è;
• ciò che sembra difficile, neanche;
• imparate a valutare positivamente gli errori (dai quali si impara molto);
• se non avete capito bene un problema, cercate di riformularlo in altri termini, oppure di riconsiderarlo sotto un aspetto diverso;
• guardatevi dalle restrizioni inconscie (che non sono enunciate nel problema); uscite dagli schemi e dagli stereotipi;
• i problemi possono avere più di una, una sola o… nessuna soluzione.
• una soluzione è anche dimostrare che un problema non ha nessuna soluzione.

Chi non ha fiducia nelle proprie capacità, ricordi: “l’intelligenza viene con una matita, un pezzo di carta… e un problema da risolvere”.

Il Puzzle, un nuovo mezzo didattico?

Osservare di persona l’interdipendenza delle forme; visualizzare determinati concetti geometrici; capire il meccanismo del ragionamento (le “catene logiche” carissime a Cartesio); sono alcune delle possibilità educative offerte dai giochi d’ingegno (puzzles in inglese). Perciò, vorremmo invitare le scuole a promuovere e ad adottare questi nuovi strumenti didattici per l’avviamento alla matematica.

Più che gioco di costruzione, il puzzle è un gioco di “ricostruzione” che richiede una buona dose di spirito deduttivo e sintetico, e conviene particolarmente bene alle persone più abili nell’imparare sperimentando (in francese: kinesthésiques).

Risolvere un puzzle non è soltanto un’attività ludico-intellettiva, ma anche la manifestazione di un’impulso primitivo, quello di riunire, catalogare, ordinare oggetti diversi; impulso che ritroviamo in alcuni uccelli, come la gazza o, meglio, l’uccello giardiniere. L’origine di questi rompicapi è dunque anche legata a questa pulsione atavica.

Riassumendo, i puzzle, chiamati enfaticamente mechanical puzzles o educational manipulatives dai pedagoghi angloamericani, incoraggiano l’esplorazione creativa e stimolano l’immaginazione facilitando la comunicazione e la cooperazione tra le persone. Last but not least, non richiedono di essere alimentati a pile, funzionano soltanto con le nostre brave cellule cerebrali!

Dunque, Cari Amici, dopo questa introduzione vi auguriamo un buon proseguimento nel mondo dei rompicapi e dei giochi matematici. Coloro che volessero saperne di più sui nostri laboratori, sui nostri servizi o prodotti, possono senz’altro contattarci.
http://www.archimedes-lab.org/italianversion1b.html

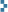
I-04 – I miei spazi

è stato molto divertente provare a ridisegnare gli spazi che mi circondano utilizzando solamente quadrati e rettangoli!
Ho usato Google Maps e Strett View per poter contornare ogni spazio, il lavoro ottenuto è bellissimo e tutto sembra un grandissimo disegno, ordinato!
Non sembra ma tutto è in armonia, tutto è ordinato e perfetto nel suo contesto!

Il rapporto aureo – Le Courbusier

Uno dei più decisi fautori del rapporto aureo e della geometria nell’arte e nell’architettura è l’architetto e pittore svizzero francese Le Corbusier.
All’inizio Le Corbusier aveva espresso idee piuttosto scettiche, per non dire negative, sull’applicazione del rapporto aureo all’arte. Ma la viva curiosità di Le Corbusier per “l’estetique” e il rapporto aureo rimanda ad almeno due dei suoi interessi precedenti: quello per le strutture sottostanti agli oggetti naturali da un lato e dall’altro, poiché proveniva da una famiglia che incoraggiava lo studio e la pratica della musica, la coscienza dell’importanza cruciale dei rapporti numerici per questa forma di armonia. La sua idea di armonia, pertanto si sviluppò cercando di trovare un qualcosa che aveva come primo effetto quello di unire , di collegare e di armonizzare il lavoro degli uomini che era diviso dalla presenza di due sistemi differenti e difficilmente conciliabili: il pollice piede degli anglosassoni e il sistema metrico dell’altra parte.

Per le sue teorie di proporzione Le Corbusier parte dallo studio dei vari monumenti antichi, costruiti secondo proporzioni e misure precise: il Partenone, i templi dell’ India, le Cattedrali erano costruiti secondo un sistema coerente, un codice: un sistema caratterizzato da un’unità essenziale. Gli strumenti che utilizzavano non erano altro che le parti del corpo umano: pollice, piede, passo….Questi erano pertanto parti integranti del corpo umano e di conseguenza adatti a servire come strumento di misura per le capanne, le case e i templi che si dovevano costruire. Ma oltre a questo, essi erano infinitamente ricchi e sottili perché facevano parte della matematica che regola il corpo umano: una matematica piena di grazia, eleganza e potenza, elemento principale di tutta l’armonia e in particolare della bellezza.
Questo architetto, dopo aver praticato un’arte dove tutto è misura, studia la natura, sotto la guida di un eccellente maestro e osserva i fenomeni molto lontano dalla sua città. Secondo lui la natura è ordine e legge, unità e diversità illimitata, raffinatezza, forza e armonia.
All’età di ventitré anni egli disegna la facciata di una casa che sta per costruire e si pone un’angosciosa domanda: “Qual è la regola che informa, che lega tutte le cose?” Si tratta di un problema di natura geometrica. La composizione delle opere d’arte è ordinata da regole, queste regole possono essere dei metodi acuti o molto sottili. Durante i suoi viaggi, Le Corbusier, aveva rilevato nelle architetture armoniose e di alta intellettualità, la costante di un’altezza di circa 2 metri e 20 e 10,2 metri tra il pavimento e il soffitto.

In seguito, durante gli anni tra il 1925 e il 1933, epoca in cui si costruiva in Francia, prima della crisi provocata dalla guerra, il gusto, il bisogno, la necessità di progettare su scala umana, l’avevano condotto a disegnare sulle pareti del suo studio una scala metrica di quattro metri di altezza, nella quale egli poteva rapportare se stesso, la propria statura e iscrivervi di traverso un insieme di misure vere, misure d’appoggio, di sosta e di passaggio. Per la creazione di questa scala di misure era partito dallo studio e dai rapporti aurei già conosciuti in precedenza.

Anche la natura è regolata dalle leggi dei rapporti geometrici: gli alberi, ad esempio, con il loro tronco, i loro rami, le loro foglie e le loro nervature, dimostrano che le leggi di crescita e di combinazione possono essere e devono essere più ricche e più sottili. Un legame matematico deve intervenire in quelle cose. E proprio da qui che Le Corbusier con i suoi assistenti, parte con i suoi studi per trovare una regola nelle proporzioni. Ed ecco che inizia lo studio per la costruzione del suo modulor.
Infatti durante il periodo estivo ordinò ad un suo giovane collaboratore di eseguire dei lavori che riguardavano appunto questa nuova teoria delle proporzioni:

“Prenda un uomo col braccio alzato di 2 metri e 20 di altezza; lo collochi in due quadrati sovrapposti di 1 metro e 10; metta a cavallo dei due quadrati un terzo quadrato che deve fornirle una soluzione. Il luogo dell’angolo retto deve poterla aiutare a situare questo terzo quadrato. Con questo reticolo di cantiere, regolato sull’uomo sistemato all’interno, io sono persuaso che lei giungerà a una serie di misure che metteranno d’accordo la statura umana e la matematica.”

Quello che sono riusciti a creare è un reticolo di proporzioni che potrà essere collocato nei cantieri della ricostruzione per fornire numerose misure armoniche utili per progettare camere, porte, armadi, finestre… “ E’ un elemento di superficie quello che noi abbiamo creato, un reticolo che mette in relazione l’ordine matematico con la statura umana. Il Modulor è lo strumento di misura nato dalla statura umana e dalla matematica. Un uomo con il braccio alzato fornisce nei punti determinanti dell’occupazione dello spazio – il piede, il plesso solare, la testa, l’estremità delle dita, essendo il braccio alzato- tre intervalli che generano una serie di sezioni auree”.
Un esempio di applicazione è VILLA SAVOYE A POISSY: in essa il Modulor regola le lunghezze, le superfici e i volumi. Mantiene dappertutto la scala umana, prestandosi a un’infinità di combinazioni e assicura l’unità nella diversità. Gli spazi si dispongono secondo proporzioni ben precise e ben studiate, che derivano dall’applicazione del suo Modulor.

La geometria nell’architettura

Secondo Ludovico Quaroni, la geometria è uno strumento col quale noi delimitiamo, tagliamo, precisiamo, formiamo lo spazio, che è il materiale di base per l’architettura.
La riconoscibilità delle forme è una condizione irrinunciabile perché il messaggio architettonico venga recepito; forme saranno dunque tanto più percepibili e riconoscibili, quanto più saranno caratteristiche e non confondibili con altre, e quindi semplici e regolari. I caratteri formali specifici, intrinseci delle figure geometriche semplici sono anzi tanto forti da generare nell’uomo, qualunque sia il grado di evoluzione al quale appartiene, immediati, istintivi riferimenti simbolici.
Si tratta degli aspetti più elementari della “psicologia della forma”, ma è proprio su questi, bene o male, che è stato possibile costruire, dall’alba dell’umanità fino ad oggi, il grande edificio unico dell’architettura universale. Senza bisogno, quindi, di riferirci esclusivamente a quelle architetture per le quali si è voluta scegliere una forma “pura”, come quella capace di dar forza alla “realtà – mito” e senza seguire le idee e le caratteristiche progettuali di Le Corbusier, in modo da considerare l’architettura solo come il gioco dei solidi geometrici, resta il fatto che è sempre possibile, salvo rarissime eccezioni, leggere in un’architettura un insieme di forme geometriche elementari.
Queste forme elementari sono le “figure” di cui si occupa la geometria classica a noi pervenuta attraverso gli scritti di Euclide.
La geometria è la scienza delle proprietà e delle relazioni di grandezze nello spazio; essa interessa dunque l’architettura in quanto si occupa delle qualità e delle proprietà delle forme spaziali, e in quanto permette operazioni grafiche bidimensionali, capaci di costruire e controllare forme tridimensionali e spaziali. La geometria interessa l’architetto come scienza – base per lo studio e la costruzione delle strutture formali. Si può dire che la geometria è la scienza che si occupa dell’economia dello spazio, usando la parola economia in senso lato, come rapporto fra quantità e qualità.
La geometria per l’architetto, è dunque una base e un mezzo disciplinare, uno strumento indispensabile nel trattamento delle forme che entrano nella composizione degli spazi. Questa geometria, per l’architetto è dunque più cose:

– da un primo punto di vista è un sistema di forme reali, risultanti dagli spazi e dalle altre configurazioni comunicanti e significanti dell’edificio costruito;
– da un secondo punto di vista, invece, è il complesso sistema grafico matematico che è stato usato per costruire sulla carta la geometria stessa degli spazi e delle altre configurazioni dell’edificio;
– infine da un terzo punto di vista, questa, è il mezzo grafico per trasmettere e comunicare, prima, durante e dopo la costruzione, l’idea progettuale e la struttura architettonica dell’edificio.

Dopo diverse analisi si può quindi dire che la geometria è una costruzione del cervello umano. Osservando la natura che ci circonda, si possono trovare certe aspetti della complessa realtà di strutture naturali, alle varie scale, dalle proporzioni del corpo umano alle simmetrie dei fiori, alle spirali del DNA. Nell’architettura il procedimento si rovescia e diventa diretto, perché ci serviamo della geometria per costruire l’organismo architettonico; e come non possiamo dire che un organismo naturale sia fatto di sola geometria, così non è possibile dire che basti la geometria per progettare un organismo architettonico. Così per prima cosa si deve evitare di considerare un’architettura tanto più valida quanto più riducibile alle forme elementari della geometria, ricordando che la verità, anche in architettura, è un fatto complesso, proprio perché cosa umana: le stesse piramidi egiziane, all’apparenza esteriore così elementari, sono il risultato di stratificazioni e complicazioni progettuali tutt’altro indifferenti. La seconda, opposta alla precedente, consiste invece nella necessità di non farsi prendere dall’illusione che progettando complicato si faccia architettura più evoluta, avanzata, moderna. Se infatti il processo non è portato avanti coscientemente e con i dovuti controlli continui si rischia di non fare architettura affatto.
La geometria, che è matematica, si occupa infatti dello spazio astratto, mentre l’architettura che è tecnica e arte, si occupa dello spazio concreto, dello spazio in rapporto all’uomo, alla sua presenza come osservatore, alla sua dimensione come fruitore.
Si può quindi arrivare alla conclusione che la necessità, per ottenere una buona architettura, è quella di raggiungere una equivalente struttura formale, cioè un insieme di rapporti dimensionali legati strettamente a loro. Ecco perché si cerca di trovare dei tentativi per codificare una legge, capace di assicurare la bellezza al manufatto architettonico: una legge dei rapporti fondamentali tra le parti e la loro riduzione all’unità, cioè al modulo ( che in latino significa misura, misura base). Tutte le civiltà, a partire dalla più antiche hanno sempre cercato di progettare le loro costruzioni sulla base di un’unità di misura astratta, il modulo, al quale sono state ricondotte per multipli e sottomultipli, le dimensioni dell’insieme e delle singole parti, anche se varia, da cultura a cultura, il modo con cui è stato trovato. La ricerca del modulo dovrebbe consistere nel misurare in tutte le sue parti un soggetto ritenuto valido, e nel cercare il massimo comune denominatore delle varie misurazioni fatte. Ci sono però anche degli edifici che traggono dalla sproporzione con le dimensioni umane, e dalle sproporzioni all’interno dell’edificio le ragioni della loro bellezza: per dare all’uomo, ad esempio, in una chiesa, il rapporto della sua persona con la divinità è necessario ricorrere alla sproporzione fra la dimensione delle parti dell’edificio più a contatto con l’uomo, volutamente tenute basse e schiacciate, e le parti fuori del contatto dell’uomo, disegnate, molto alte, slanciate, eleganti, elevate.
Le proporzioni ognuno deve trovarle da se, perché solo in questo modo le proporzioni, o le sproporzioni, adatte a esprimere l’idea progettuale. I moduli e le proporzioni degli ordini classici, comunque, costituiscono un sistema modulare statico e soddisfacevano benissimo le esigenze dell’architettura classica e delle molte sue derivazioni. Le proporzioni classiche sono armoniche, mentre la civiltà attuale è spesso caratterizzata da disarmonie. Probabilmente solamente le dissonanze, in architettura, e le sproporzioni, riescono a rendere l’atmosfera dinamica, tragica, scomposta del mondo attuale; tuttavia in tempi recenti, l’attenzione degli architetti e in particolare di Le Corbusier, è stata attratta dalle ricerche fatte dai matematici sulle proporzioni dinamiche e in particolare sulle proprietà del rapporto aureo. Il rettangolo che si ottiene avente come lato corto la sezione aurea del lato lungo, ha la proprietà di riprodurre la stessa proporzione fra i lati dei due rettangoli che si ottengono quando sia tagliato a metà e questa proprietà risulta molto vantaggiosa nella pratica del progettare, come d’aiuto è la conoscenza della sezione aurea e della sua facile costruzione, perché permette di tagliare una dimensione (una facciata, una piazza, una stanza…) in due parti che sono molto diverse fra loro, ma non troppo diverse.

L’ARMONIA DELLA REGOLA AUREA

Come base dell’armonia il filosofo greco Filolao poneva la “discordanza concorde”, vale a dire l’accordo di consonanze ineguali rappresentate da proporzioni dissimili, come il rapporto fra 3 e 4 o fra 2 e 3. Il suo maestro Pitagora aveva scoperto che le armonie musicali si devono a rapporti di piccole unità numeriche (come ad esempio il triangolo platonica).

Con il pensiero cristiano le convinzioni pitagoriche vengono integrate con alcuni passi biblici: nella Genesi viene indicata la misura dell’arca di Noè e anche il Tempio di Salomone viene indicato con misure e proporzioni precise. Queste, pertanto, sono tutte immagini simboliche dell’universo basate su relazioni proporzionali, in sintonia con il pensiero cristiano: “Dio ha disposto tutto con misura, numero e peso”.Che cos’hanno in comune la mirabile disposizione dei petali di una rosa, il celebre dipinto di Salvador Dalì il “sacramento dell’ultima cena”, l’armoniosa spirale di alcune conchiglie e l’allevamento di conigli?

Queste realtà così disparate condividono un numero. O una proporzione geometrica, noti fin dall’antichità e designati nell’Ottocento con una serie di definizioni che alludono all’oro, simbolo di ciò che è nobile, inalterabile e prezioso: “numero aureo, rapporto aureo e sezione aurea”.
Il sostantivo proporzione per indicare un rapporto tra cose considerate secondo la grandezza o la quantità; oppure un rapporto tra cose o parti di esse che appaia caratterizzato da una particolare armonia. In matematica con proporzione si intende di solito un’uguaglianza come 9 sta a 3 come 6 sta a 2. Il rapporto aureo è un interessante amalgama dei due significati, quello quantitativo e quello estetico, perché pur essendo definito matematicamente gli viene attribuita la capacità, se applicato a oggetti che colpiscono i sensi, di renderli piacevolmente armoniosi.

La prima chiara definizione del rapporto che sarebbe stato chiamato aureo fu formulata dal fondatore della geometria in quanto sistema deduttivo: Euclide. Egli si è soffermato su un particolare rapporto di lunghezze, ottenibile in modo relativamente semplice dividendo una linea secondo quella che chiamò la sua proporzione estrema e media. Il valore esatto del rapporto aureo corrisponde al numero 1,6180339887…., con infinite cifre decimali prive di sequenze ripetitive; un numero interminabile che ha incuriosito gli uomini fin dall’antichità. Il fatto che la sezione aurea non si possa esprimere per mezzo di una frazione ( cioè con un numero razionale) significa semplicemente che è impossibile trovare due numeri interi il cui rapporto corrisponda esattamente al rapporto di due lunghezze.

Il simbolo consueto per indicare il rapporto aureo è la lettera τ (tau) dal greco taglio, sezione. Ma all’inizio del XX secolo il matematico americano Mark Barr ha introdotto, al posto di tau, la lettera greca φ (phi), dall’iniziale del nome del grande scultore Fidia vissuto tra il 490 e il 430 a. C. Fidia aveva spesso applicato consciamente e con grande precisione, il rapporto aureo alle sue opere.

Ma il rapporto aureo non ha affascinato solo i matematici. Biologi, artisti, musicisti, storici, architetti, psicologi, perfino mistici hanno indagato e discusso la sua inattesa presenza nei campi più diversi.

Il rapporto aureo può essere scoperto non solo nei fenomeni naturali, ma anche in molte opere dell’uomo, in particolare in campo artistico. Il rapporto aureo compare nelle opere di molti artisti, architetti e progettisti, e perfino in molte celebri composizioni musicali.
Una delle proprietà che contribuiscono alla riuscita estetica di un’opera è il suo essere proporzionata: l’armonia del rapporto quantitativo, sia delle parti tra loro sia delle parti col tutto.

GLI ANTICHI…

Molti autori insistono sul fatto che le dimensioni della Grande Piramide si basino sul rapporto aureo. Ma sorge spontanea una domanda: i sudditi del faraone sapevano davvero dell’esistenza di φ? Solo attraverso una serie di misurazioni si è arrivati a pensare che gli antichi greci erano a conoscenza del rapporto aureo. Ma è quasi impossibile provare che il rapporto aureo non compaia in qualche manufatto egizio, finchè la dimostrazione è data solo da alcune misurazioni. In mancanza di documenti che attestino l’uso consapevole del rapporto aureo, le dimensioni dell’opera d’arte o del progetto architettonico dovrebbero esser tali che la presenza di φ si imponga all’osservatore per la sua evidenza; al contrario, se esso appare quasi nascosto nelle pieghe della struttura visibile, cosicchè solo un’analisi molto elaborata riesce a rivelarlo, è difficile convincersi che la sua presenza sia frutto della volontà dell’artista o dell’architetto.

Studiosi come Piazzi Smith e Taylor pensano che la Grande Piramide di Cheope contenesse una serie di proporzioni basate su conoscenze matematiche ignote agli egizi. Secondo Erodono, la piramide fu costruita in modo tale che l’area di ciascuna faccia fosse uguale all’area di un quadrato il cui lato sia pari all’altezza della piramide. Negli anni successivi, altri diversi autori sostenevano la stessa tesi. Questa teoria porta alla conclusione che la Grande Piramide è stata progettata in modo tale che, dividendo l’altezza di una faccia triangolare per la metà di uno dei suoi lati della base si ottenga il rapporto aureo. Attraverso una serie di analisi sono arrivati a scoprire che la base della piramide è molto vicina ad essere un quadrato perfetto: i suoi lati variano da un minimo di 230.25 metri, a un massimo di 230.45 metri. L’altezza del monumento è di 146.73 metri. Da questi valori, usando il teorema di Pitagora, ricaviamo l’ipotenusa 186.54 metri. Perciò si ha che il rapporto tra l’ipotenusa e la metà del lato alla base della piramide è uguale 1.62 un valore molto vicino al nostro φ. A questo punto si può concludere, anche se non con estrema certezza che gli architetti egiziano conoscessero il rapporto aureo, non solo perché tale rapporto è annidato nei rapporti della Grande Piramide, ma anche per la testimonianza del grande Erodoto.

IL RETTANGOLO AUREO

Nel rettangolo aureo il lato maggiore e il lato minore stanno tra loro in un rapporto pari a φ. Immaginiamo di sottrarre da questo rettangolo un quadrato di lato uguale al minore. Il risultato sarà un piccolo rettangolo, che a sua volta sarà un rettangolo aureo.

Le dimensioni del rettangolo “figlio” sono minori di quelle del rettangolo “genitore” di un fattore pari a φ. Togliendo un quadrato dal rettangolo “figlio2 con lo stesso procedimento, otteniamo un terzo rettangolo aureo di nuovo rimpicciolito di un fattore pari a φ. Proseguendo si genera una serie di rettangoli aurei sempre più piccoli, di dimensioni ridotte ogni volta di un fattore uguale a φ. Esaminando ciascun rettangolo, si può constatare che sono identici. Quello aureo è l’unico rettangolo che consente, togliendo un quadrato della sua area, di ottenere un rettangolo simile al primo. Tracciando due diagonali che si intersecano in ciascuna coppia di rettangoli, “genitore” e “figlio”, si trova che tutte le diagonali passano per un punto. Si può dire, quindi, che una serie geometrica di rettangoli aurei sempre più piccoli “converga” intorno a quel punto senza mai raggiungerlo. (Tale punto, visto che ha le proprietà divine del rapporto aureo è stato definito “occhio di Dio”).

Geometria con i blocchi colorati – Barbara Bando Irvin

Per gli insegnanti risulta spesso molto difficile spiegare ai bambini alcuni concetti matematici e geometrici, poiché essi sono astratti e lontani dalla realtà esperienziale. Questo libro rappresenta un valido strumento per avvicinare i bambini alla scoperta delle forme geometriche e alle relazioni tra di loro; esso propone una serie di schede fotocopiabili e una serie di blocchi colorati, di forme e colori diversi, che con la loro concretezza e facilità di manipolazione , integrano e supportano l’apprendimento di concetti e nozioni geometriche.
Il testo è consigliato dalla terza elementare in poi e può essere usato non solo per consolidare conoscenze geometriche ma anche per sviluppare ulteriormente le abilità di risoluzione di problemi e maturare altrettante abilità logiche e matematiche.
Le attività in esso contenute, presentate sotto forma di gioco, invitano l’alunno a costruire, suddividere e ricomporre le forme; grazie all’utilizzo dei blocchi colorati le nozioni vengono consolidate anche grazie al supporto visivo.

STRUTTURA DEL TESTO

I blocchi colorati allegati al testo sono 100, di sei forme e colori diversi: esagoni gialli, trapezi rossi, rombi blu e marroni, triangoli verdi e quadrati arancioni; tutti i blocchi colorati hanno i lati che misurano la stesa lunghezza ( ad eccezione del lato maggiore del trapezio che misura il doppio).

Una delle prime pagine del testo presenta delle griglie con disegnati i blocchi colorati, così che, fotocopiando la pagina, ogni alunno, ritagliando e colorando, può crearsi la propria serie di blocchi colorati. Questa potrebbe essere un’attività molto importante perché l’alunno andrebbe alla scoperta delle forme e di come si possono combinare per dar vita ad altre forme diverse. Inoltre l’aiuto del colore facilita l’individuazione di una specifica forma.
Le pagine successive presentano invece una serie di griglie isometriche, a linea continua e tratteggiata, che possono essere usate per aiutare gli alunni a scoprire le relazioni geometriche, giocare con le frazioni e creare figure con la propria fantasia.
Il resto del libro è diviso in due parti: la prima parte è dedicata alla geometria e la seconda alle frazioni.
Ogni parte presenta un vocabolario che contiene i termini fondamentali del capitolo, suggerimenti all’insegnante su come preparare lo svolgimento della lezione e degli esercizi specifici; gli esercizi sono mirati a sviluppare diverse capacità e si prefiggono di raggiungere i seguenti obiettivi:

per la geometria
-distinguere e classificare i blocchi colorati
-formare nuove figure a partire dalle figure di base
-conoscere il concetto di similitudine e individuare figure congruenti
-ingrandire le figure in modo proporzionale
-costruire figure simili con i blocchi
-conoscere il concetto di perimetro e area delle figure
-conoscere la simmetria nelle figure e tracciare assi di simmetria
-scoprire le immagini riflesse allo specchio e riconoscere quelle della
stessa forma o grandezza
-applicare movimenti di trasformazione
-conoscere, classificare e misurare gli angoli
per le frazioni
-individuare le parti frazionarie di un insieme
-individuare le parti frazionarie di un blocco colorato
-frazionare la parti di un esagono
-identificare e illustrare le frazioni unitarie, proprie ed equivalenti
-sommare numeri interi con frazioni
-sommare frazioni con denominatori comuni e diversi.
Le ultime pagine presentano le soluzioni di tutti gli esercizi.

PERCHE’ USARE QUESTO LIBRO??

Sfogliando e analizzando il testo, abbiamo trovato come esso presenti tantissimi aspetti positivi che ci hanno spinto a ritenerlo un libro molto utile e da poter usare con i nostri futuri alunni.
Innanzi tutto il testo è innovativo in quanto suggerisce una modalità di insegnamento nuova, più attiva e partecipativa da parte degli alunni, che di conseguenza si dimostreranno più interessati e coinvolti. La partecipazione degli alunni più attiva e interessata deriva anche dal fatto che questa modalità di insegnamento propone le attività sotto forma di gioco. Apprendere attraverso il gioco aiuta a concentrarsi meglio, collaborare e ricordare più facilmente. La partecipazione degli alunni è anche stimolata dalla manipolazione dei blocchi; la loro concretezza aiuta la comprensione e la fissazione di ciò che si apprende.
Le forme e i colori dei blocchi stimolano la memoria visiva degli alunni, che grazie a questi strumenti saranno successivamente in grado di ricordare nozioni e concetti più o meno complessi.
Le attività proposte possono essere svolte singolarmente da ciascun alunno, anche come modalità di verifica, ma possono anche essere svolte da piccoli gruppi di alunni per stimolare la partecipazione e il confronto con le idee altrui.
Apprendere attraverso il gioco e la concretezza dei blocchi facilita così l’apprendimento in tutti gli alunni, soprattutto con quelli in difficoltà; questa modalità di insegnamento dunque può essere così usata anche in classi con alunni in difficoltà: essi apprenderanno più facilmente mentre i compagni svilupperanno ulteriori abilità.
Anche la struttura stessa del libro è considerata per noi un punto di forza; il vocabolario aiuta le insegnanti a preparare gli alunni ai termini che verranno usati nelle attività, i suggerimenti per la preparazione delle attività permettono agli insegnanti di organizzare una lezione senza andare incontro ad inconvenienti, le attività proposte aiutano gli insegnanti a rispondere in modo adeguato ai quesiti degli alunni.
La suddivisione del testo per argomenti è un valido aiuto per gli insegnanti che possono così organizzare percorsi didattici tappa per tappa; anche le soluzioni in fondo al testo sono utili perché permettono di chiarire ogni dubbio.
Proporre attività con i blocchi colorati aiuta a sviluppare l’abilità di problem solving e la fantasia: incoraggiare infatti gli alunni a dar vita a nuove forme e figure, accresce la capacità di immaginazione e risoluzione di problemi.
Inoltre il testo presenta molti legami anche con concetti aritmetici e può quindi essere usato ricorrendo a collegamenti con ciò che si è già imparato in matematica.
Non va infine dimenticato come le attività qui descritte si accompagnino sempre al piacere della scoperta, che stimola la volontà e l’interesse per i successivi apprendimenti.

L’unico punto di debolezza da noi individuato è che presenta pochi legami con la realtà; in effetti questo si può constatare però è anche vero che sta all’insegnante creare anche con questo tipo di insegnamento i collegamenti con la realtà esterna, in modo da insegnare una vera geometria i cui blocchi colorati si posso scoprire anche nella nostra quotidianità.

Concludendo possiamo dire che in generale questo testo è molto utile perché consente lo sviluppo delle capacità do esplorazione, osservazione e costruzione che sono la base dell’incremento di una capacità fondamentale per il nostro apprendimento: la metacognizione; saper conoscere il proprio pensiero e monitorarlo sono abilità che possono essere accresciute anche grazie all’uso dei blocchi colorati e delle attività proposte nel testo per l’apprendimento della geometria.